CodeChef starters are a series of competitive programming contests conducted by CodeChef. There are 4 contest tiers for users with different ratings: easiest being Division 4 and hardest being Division 1.

Problems

There were 7 rated problems for Division 4. Depending on how quickly you solve and how many problems are solved correctly you are assigned contest ranking. Based on your ranking, user rating goes either up or down. Starters57 had 24k participants. The contest was three hours long.

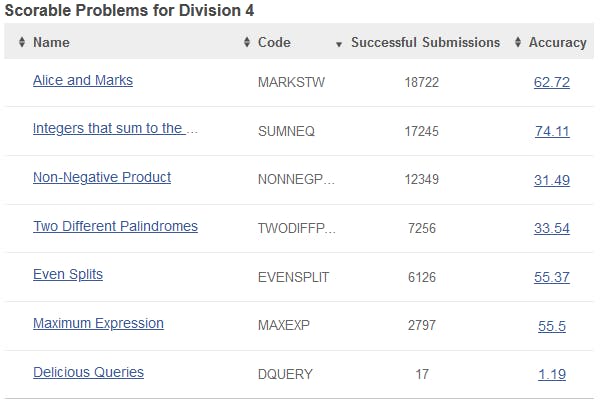
Alice and Marks

Problem

• There are two students named Bob and Alice. Alice has scored X marks and Bob has scored Y marks, in the same exam. Alice is happy if she gets at least double the marks Bob gets. Given X and Y, determine whether she is happy or not.

Input

• Only one line of input, containing two space separated integers X and Y; X ->Alice, Y -> Bob

Output Format

• Yes if Alice is determined to be happy with given (X,Y), No if Alice unhappy.
• Case insensitive output, so yes, YES, YeS and yEs all valid outputs.

Constraints

• 1 ≤ X ≤ 100
• 1 ≤ Y ≤ 100

Sample

If input is: 5 2

X = 5 and Y = 2

As Alice's marks (5) are more than twice of Bob's marks (2) , the output is YES

Algorithmic solution

Input : x y
if (x >= (2y))
  output: Yes
else
  output: No

Take care Alice wants at least twice, and so if X is double of Y output is yes.

Code solution (c++)

#include <iostream>
#include <bits/stdc++.h>
#include <vector>
using namespace std;
int main(){
  ios_base::sync_with_stdio(false);
  cin.tie(NULL);
  int t ;
  int x,y;
  cin>>x>>y;
  if (x >= 2*y)
    cout<<"Yes\n";
  else
    cout<<"No\n";
  return 0;
}

Integers summing to same number

Problem

• Alice has a number N. She wants to know how many pairs of positive integers exist whose sum is N.
• If N is 3, 2 pairs exist [ (1,2), (2,1) ]

Input

• Only one line of input, containing a single positive integer N.

Output

• Output the number of ordered pairs of (i,j), where i+j == N.

Constraints

• 1 ≤ N ≤ 100

Sample

• If N = 4, pairs that can be formed are (1,3), (3,1), (2,2) .

Algorithmic Solution

While there may be an iterative solution to individually count each pair using loops, it's not necessary. Care should be taken to examine the output requirement: it's not necessary for us to generate or output the pairs. It's only necessary to count the number of pairs that can be formed. Creating general test cases and solving them manually can help us come to the result easily.

For N = 1, `0` pairs can be formed.
For N = 2, `1` pair can be formed:  (1,1).
For N = 3, `2` pairs can be formed :(2,1) and (1,2).
For N = 4, `3` pairs can be formed: (1,3), (3,1), (2,2).
....
...
For N = k, k-1 pairs can be formed; 
viz, for a positive number N,  N-1 pairs of positive numbers sum up to N.

Code Solution (C++)

#include <iostream>
#include <bits/stdc++.h>
#include <vector>
using namespace std;
int main(){
  ios_base::sync_with_stdio(false);
  cin.tie(NULL);
  int n ;
  cin>>n;
  cout<<n-1<<"\n";
  return 0;
}

Non Negative Product

Problem

• Alice has an array of N integers. She wants to find the minimum number of items she has to remove from the array to get a non-negative product of all array elements.

Input

• First line of input contains integer t, where t signifies number of test cases.
• First line of each test case contains number N.
• Second line of input contains N space separated integers. (N integers)

Output

• For each test case, output on new line the minimum number of elements that need to be removed from array to get a non-negative sum.

Constraints

• 1 ≤ t ≤ 100
• 1 ≤ N ≤ 10000
• -1000 ≤ A_i ≤ 1000

Sample

For sample input :

4
3
1 9 8
4
2 -1 9 100
4
2 -1 0 100
4
2 -1 -1 100

t = 4, so 4 test cases

Test case 1

• N = 3
• A = [ 1, 9 ,8 ]
• As product of all A_i elements is 72, which is positive, 0 items need to be removed for non-negative output, so output 0.

Test case 2

• N = 4
• A = 2, -1, 9, 100
• There are odd number of negatives in array, so we need to remove 1 element(-1) to make product non-negative. Output 1.

Test case 3

• N = 4
• A = 2 -1 0 100
• This case is special, because 0 is part of array. Whatever the array elements, if zero is multiplied, the answer is always zero(non-negative). Therefor output is zero.

Algorithmic Solution

• It is necessary to take N elements and store them in A.
• Count the number of negative elements of A in K;
• If K_negative is even, the product will be non-negative (because negative * negative is positive).
• If K_negative is odd, we need to remove 1 element to make K even and product non-negative.
• Special Case : If 0 part of array elements, product will always be 0.

input t:
loop t times : {
  input N;
  take input of N integers in Array A;
  sort array A; 
  c = 0;
  iterate over A elements as long as Ai is negative{
    if c is even
         make c = 1;
    else if c is odd
         make c = 0;
    i = i+1;
  }
  if Ai is 0:
    output 0;
  else
    output c;
}

One might assume at first glance that we need to count the total number of negatives in the array of items, but we are only concerned with the sign. Thus instead of endlessly incrementing the count of negatives, we set c = 0 whenever the number of negatives is even. If number of negatives is odd , we set c = 1.

Sorting makes the solution faster because N can go upto 10⁵. Assuming we didn't sort the array, we would have to check every single item of the array for its sign (+/-). In our solution, the maximum item checked is 0: once positive is encountered loop breaks.

Also, carefully note that we do not need the product, so don't even attempt to calculate it. The worst case product of 10⁵ numbers between [-1000,1000] cannot be stored in our data types.

Code Solution (C++)

#include <iostream>
#include <bits/stdc++.h>
#include <vector>
using namespace std;
int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    int t,n,i,c;
    cin>>t;
    while (t--){
      cin>>n;
      vector <int> items(n,0);
      for (i = 0; i<n;i++){
        cin>>items[i];
      }
      sort(items.begin(), items.end());
      i = 0,c = 0;
      for (i = 0; items[i]<0;i++)
        c = (c+1)%2;
      if (items[i]==0)
        cout<<0<<"\n";
      else
        cout<<c<<"\n";
  }
}

Two Different Palindromes

Problem

• Given two positive integers A and B, determine if it is possible to construct two different binary strings.
• Binary strings are strings consisting of only zeroes and ones.
• The two strings should satisfy the following properties

• Both strings should be palindromes.

• There should be exactly A 0's and B 1's in each string.

• A palindrome string is one whose reverse is equal to itself, eg 1001 reversed is 1001.
• For two strings to be different they should differ by at-least 1 character.

Input

• First line of input contains T, the number of test cases.
• Each case contains a line of two space separated integers A and B

Output

• Yes if it is possible to construct two binary strings under given constraints for A and B.
• No if it is not possible to construct two binary strings satisfying requirements.

Constraints

• 1 ≤ T ≤ 10⁵
• 1 ≤ A ≤ 10⁶
• 1 ≤ B ≤ 10⁶

Sample

• If A = 2 and B = 2, answer is YES (possible strings are 1001 and 0110).
• If A = 3 and B = 3, answer is NO (No way to combine 111000 to get even one palindrome string).
• If A = 2 and B = 3, answer is YES(possible palindrome strings 01110, 10101)

Algorithmic Solution

• As we do not actually need to output the binary strings, there is no need to calculate the strings. A little bit of test case observation will lead us to the answer.

  If A = 1 and B = 1, answer is No 
  If A = 1 and B = 2, answer is No
  If A = 2 and B = 2, answer is Yes : 1001 & 0110
  If A = 1 and B = 4, answer is No
  If A = 3 and B = 2, answer is Yes : 01010 and 10001
  If A = 3 and B = 3, answer is No
  If A = 4 and B = 4, answer is Yes : 11000011 & 00111100 (among others)
  

  Notice that
• whenever the sum of A and B is 3 or less, it is not possible to conduct two different requirement strings.
• whenever A = 1 or B = 1, it is not possible to construct two different requirement strings.
• if both A and B are odd, answer is NO
• If all above conditions are false, answer is Yes, i.e if

  (A+B > 3 && A is not 1 && B is not 1 && A and B are not both odd )

Code Solution (C++)

#include <iostream>
#include <bits/stdc++.h>
#include <vector>
using namespace std;
int main(){
  ios_base::sync_with_stdio(false);
  cin.tie(NULL);
  int t,a,b;

  cin>>t;
  while (t--){
    cin>>a>>b;
    if (a<=1 || b<=1 ||a+b<=3)
      cout<<"No\n";
    else {
      //if both odd then No
      if ((a&1)&&(b&1))
        cout<<"No\n";
      else  
        cout<<"Yes\n";
    }
  }
}

Even Splits

Problem

• A subsequence of a string is a string that can be derived from given string by deleting some or no elements without changing order i.e ABD is a subsequence of ABCDEF.
• Given a binary string of length N.

• We can perform the following operation on string:

  Pick any even length subsequence: supposing the chosen subsequence has length 2k, move first k characters to the beginning of S and the other k to the end of S (without changing order of either first k or last k)

• Suppose S = 0101

  if chosen subsequence is 01(last two).

  Move 0 to beginning, 1 to end to get 0011.

• What is the lexicographically smallest string that can be obtained after performing this operation several (possibly zero times)?

• Here lexicographically signifies dictionary order. In a dictionary, abe comes before ace, because the first non-equal character (b) of abe is smaller than (c). For binary strings, only 0 and 1 are characters. So the smaller binary string will contain 0 at an ith position for which the other string contains 1.

Input

• First line of input contains integer T, the number of test cases.
• For each test case
• • the first line contains single integer N, size of binary string
• • the second line contains binary string of length N

Output

• For each test case, output on a new line the lexicographically shortest binary string possible after performing allowed operation any number of times.

Constraints

• 1 ≤ T ≤ 10⁵.
• 1 ≤ N ≤ 2 . 10⁵.
• S is a binary string.
• The sum of N across all test cases won't exceed 2 * 10⁵.

Sample

• Sample Input

  4
  2
  10
  4
  1001
  5
  11111
  7
  0010100
  

• Sample Output

  10
  0011
  11111
  0000011
  

Algorithmic Solution

• At first glance, the shown operations seem difficult. Have to take an a binary string, perform operations on it's subsequences, and also determine final string.
• The complex way the problem is explained is a red herring (misdirection). The allowed operation allows us to completely change the given string. Examine the sample output carefully: every single one has the containing zeroes to the left and 1's to the right. This is because the smallest dictionary order binary string will have all zeroes to the left, and 1's to the right.
• The one exception is the string 10, which remains as it is. Why? The chosen subsequence for 10 is 10, and moving 1 to the start and 0 to the end gives the same output, 10. Thus for 10 input, output is also 10.

  All we have to do in the problem is take the string, sort it, and output the sorted string. But if the string is 10, output 10. ```

Code Solution (C++)

#include <iostream>
#include <bits/stdc++.h>
#include <vector>
#include <string>
#include <algorithm>
#include <map>
#include <list>
using namespace std;
int main(){
  ios_base::sync_with_stdio(false);
  cin.tie(NULL);
  int t,i,n;
  cin>>t;
  while (t--){
    cin>>n;
    cin.ignore();
    string s;
    std::getline(cin,s);
    if (n>2)
      sort(s.begin(), s.end());
    cout<<s<<"\n";
  }
}

Maximum Expression

Problem

• Given a string S of length N, containing digits 0-9 and characters '+' a '-'. S is a valid mathematical expression.
• Rearrange the characters of S to form a valid mathematical expression such that the mathematical value of the expression is maximum

Input

• First line of input contains integer T, the number of test cases.
• Each test case contains two lines of input:
• The first line contains single integer N, the size of string
• The second line contains string S

Output

• For each case, output on new line the rearranged string giving maximum value upon evaluation. Multiple correct answers allowed (if multiple answers exist).

Constraints

• 1 ≤ T ≤ 1000
• 3 ≤ N ≤ 10⁵
• S only has characters from (0123456789+-)

Sample

• Sample Input

  3
  7
  4-89+20
  5
  5-9+0
  3
  9-5
  

• Sample Output

  984+2-0
  5+9-0
  9-5
  

Algorithmic Solution

• To generate the maximum possible expression, our first digit needs to be as big as possible.
• Thus, we need to count the occurrence of each digit, and make sure the maximum values come first.
• There are three steps to create expression: form the biggest number, add some numbers, subtract some numbers.
• For example, if input is 4+9-28+3, the maximum possible expression is 98+4+3-1. Thus the numbers occur in decreasing order. The number of pluses and minuses of original expression are maintained: addition is done first and then subtraction.
• The no of digits of the first number is equal to the total number of digits minus the number of operations (i.e sum of pluses and minuses).

  input: test cases t
  iterate t times {
  input : integer N;
  input: string S of size N;
  m = 0, p = 0; 
  //m for no of pluses , p for no of minuses
  iterate over every character c in S{
      if c is +,
        p = p +1  ;
      if c is - 
        m = m + 1;
      if c is a digit
        increase count of that digit by 1
        increase the count of digits by 1
  }
      j = d - (p+m); 
  /* if number of digits is 5, and number of operations is 2, the first number will have three digits */
      while (j){
    output next largest digit available
        j = j -1;
      }
    while (p){
  output "+"
  output next largest digit
  p = p -1;
    }
  while (m){
  output "-"
  output next largest digit
  m = m-1;
    }
  output newline_character
  }
  

Code Solution (C++)

#include <iostream>
#include <bits/stdc++.h>
#include <vector>
#include <string>
using namespace std;

int main(){
  ios_base::sync_with_stdio(false);
  cin.tie(NULL);
  int t,m,p,i,j,d,n,k;
  string s;
  cin>>t;
  while (t--){
    cin>>n;
    vector <int> nos(10,0);
    cin>>s;
    m = 0,p = 0,i = 0,d= 0;
    for (char c = s[i]; i < n;i++){
      c = s[i];
      if (c=='-')
        m++; 
      else if (c=='+')
        p++;
      else{
        nos[c-'0']++;
        d++;
      }
    }
    i = 9;
    j = d - (p+m);
    while (j){
      while (nos[i] == 0){
        i--;
      }
      cout<<i;
      nos[i]--;
      j--;
    }
    while (p){
      while (nos[i] == 0){
        i--;
      }
      cout<<"+"<<i;
      nos[i]--;
      p--;
    }
    while (m){
      while (nos[i] == 0){
        i--;
      }
      cout<<"-"<<i;
      nos[i]--;
      m--;
    }
    cout<<"\n";
  }
}

Conclusion

Problem solving is a skill like any other. With practice and consistency, one improves. Do not be disheartened if you are unable to solve any question. Personally, I was able to solve only 3 out of the seven questions during the contest. The next day, after the contest, I kept trying and managed to solve two more without any external help. I solved the maximum expression problem, after reading the editorial and understanding the logic involved. Contests may be like exams, but you get more than one chance. Keep going✊!